|
|
Construction de la trajectoire d'une particule chargée soumise à une force créée par une charge fixe. |
|
|
Construction de la trajectoire d'une particule chargée soumise à une force créée par une charge fixe. |
On s'intéresse ici à l'utilisation de la méthode d'Euler et aux capacités de Cabri Géomètre pour résoudre le problème posé par les forces coulombiennes.
Le principe fondamental de la dynamique F=ms
dv/dt
et l'expession de la force électrostatique F=k q q' / r2 r/r
permettent de déterminer la trajectoire d'un objet de masse
m de charge q dans le champ électrostatique créé par la charge q' .
Pour une approche plus complète de la méthode d'Euler, on lira avec le plus grand profit les articles
de Dominique Tournès et Daniel Courounadin sur le site web de Yves Martin : http://www-cabri.imag.fr/abracadabri/Courbes/EquaDiff/EDiffGene.html
http://www-cabri.imag.fr/abracadabri/Coniques/UtilizConik/EulerPlanet/EulerPlanet.html
L'approche des constructions présentées ici correspond à l'esprit du nouveau programme de
Sciences Physiques de 2002 : " ... calculer et prévoir l'évolution temporelle d'un système
mécanique une fois connue les forces mises en jeu et les conditions initiales." Groupe d'Experts
Physique Chimie Février 2001.
Méthode d'Euler ordre 1
Les relations importantes :
Force électrostatique subie par la charge q de masse m située au point M
: F = 9.0e9 q q' / r2 r/r, la force est attractive dirigée vers le noyau N portant
la charge q', si q et q' sont de signe contraire, ou dirigée dans la direction NM si q et q' sont de même
signe.
Dans l'expérience initiale de Rutherford, q est un proton, et q' un noyau d'or (force répulsive).
F = m a = m dv/dt et F = 9.0e9 q q' / r2 r/r soit a = 9.0e9
q q' /( m r2 ) r/r
r1 = ro + vo dt (ou dr = v dt) au premier ordre
v1 = vo + ao dt
Unités : Les grandeurs utilisées ici ne sont pas adaptées aux dessins, aussi les variables
seront le nombre de charges élémentaires (1,6e-19C), les distances en femtomètre (10-15m)
et les masses exprimées par rapport à la masse d'un électron (me=9,11e-31kg).
L'accélération s'écrit alors a = 2.52e32 qN qM / (nme r2) où
qN = q / 1,6e-19C pour le noyau,
qM = q / 1,6e-19C et nme = masse / 9,11e-31kg pour la charge mobile
r = distance (NM) en femtomètre.
Valeurs typiques : qN = 79, qM = 1, nM = 1835, r = 100 fm
Construction :
- Tracer 4 segments, sur des droites horizontales, qui représentent qN , qM, nme, et l'intervalle de
temps dt.
On utilisera la longueur de ces segments comme paramètres dans les calculs suivants, (multipliés
éventuellement par un coefficient pour les échelles).
- Placer les points N (Noyau) et Mo (position initiale dde la charge q)
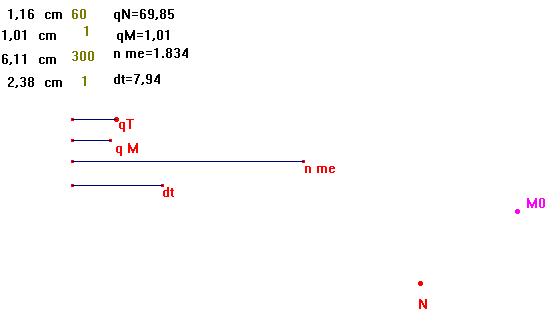
- Tracer le vecteur vo, vitesse initiale du point Mo.
Ce vecteur peut avantageusement être créé autour d'un point fixe afin de rendre
sa manipulation plus facile. Il faut alors le reporter en Mo.
- Mesurer la distance ro=distance (T Mo) et la longueur vo du vecteur vo.

- Calculer ao= 2.52e32 qN qM / (nme r2) et comme on obtient un nombre très grand (1025 à 1028 environ), on multiplie ce résultat par 10-27 par exemple. De même la vitesse sera multipliée par un coefficient, (10 000 000 pour 1cm = 10 000 km/s)
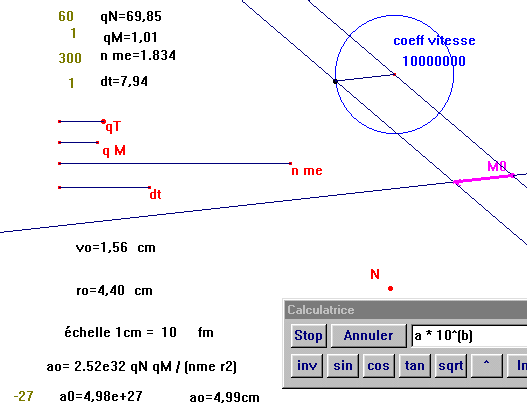
- Tracer la demi-droite (Mo N), pour définir la direction du vecteur Fo.
- Calculer la grandeur vo dt, et la reporter sur la demi-droite (Mo vo), pour définir le point M1
r1 = ro + vo dt (ou dr = v dt)
- Calculer la grandeur ao dt, et la reporter sur la demi-droite (Mo N') où N' est le symétrique
de N par rapport à Mo, pour définir le vecteur (ao dt)
v1 = vo + ao dt
v1 est obtenu par addition vectorielle de vo et ao dt au point M1.
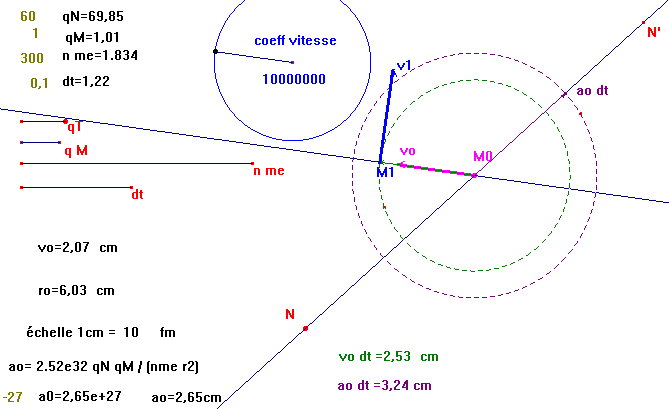
- Mesurer la grandeur obtenue r1 pour calculer a1= 2.52e32 qN qM / (nme r12) , et recommencer....
pour le couple (M1, v1)....... ou plus simplement définir une macro.
| Définition de la macro construction EulerQ1 : ( Q charge (Coulomb), 1 pour 1 vecteur) |
| Objets initiaux : qN, qM (nb de charge en unité 1.6e-19C), nme = masse de la particule mobile en unité de masse de l'électron 9.11e-30kg), dt (unité de temps d'intégration), xx=echelle des longueurs 1cm=xx fm(= xx e-15m), nb entier coeff de calcul graphique des accélérations (environ -27), point N, point M0, vecteur Vo |
| Objets finaux : point M1, vecteur v1 |
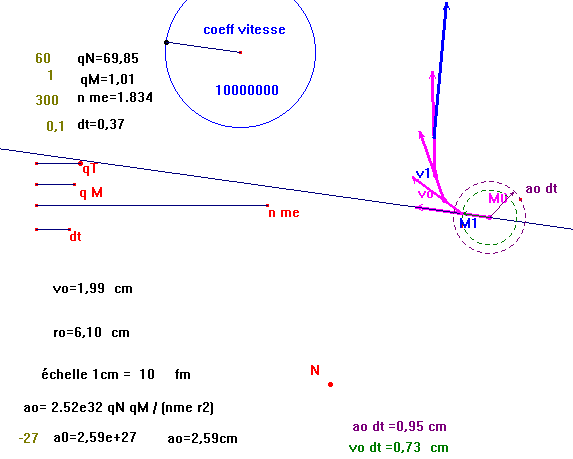
A partir de cette macro, on peut en définir une seconde qui trace 4 points successifs et la conique définie
par les 5 points Mo à M4 (avec l'outil Conique de Cabri).
| Définition de la macro construction EulerQ1_4pv_cnk.mac : ( Q charge (Coulomb), 1 pour ordre 1) |
| Objets initiaux : qN, qM (nb de charge en unité 1.6e-19C), nme = masse de la particule mobile en unité de masse de l'électron 9.11e-30kg), dt (unité de temps d'intégration), xx=echelle des longueurs 1cm=xx fm(= xx e-15m), nb entier coeff de calcul graphique des accélérations (environ -27), point N, point M0, vecteur Vo |
| Objets finaux : M1 à M4 et vecteur v1 à v4 et la conique des 5 pts M0 à M4 |
Après un peu de nettoyage,
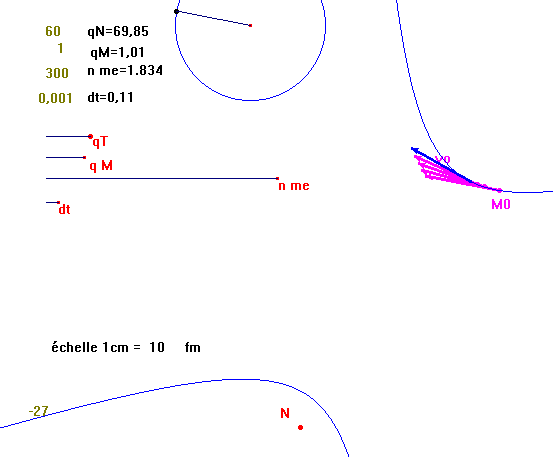
ou bien avec tous les éléments de la construction,
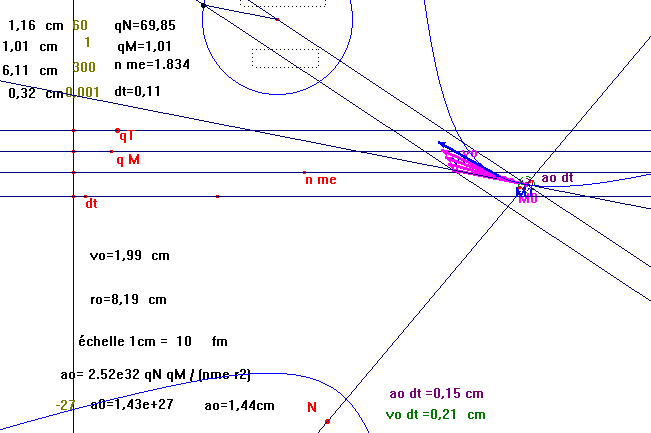
Pour placer plusieurs (10) points on peut définir la macro
| Définition de la macro construction EulerQ10v.mac : ( ordre 1, Q Coulomb, 10 pour les 10 points et vecteurs vitesses) |
| Objets initiaux : qN, qM (nb de charge en unité 1.6e-19C), nme = masse de la particule mobile en unité de masse de l'électron 9.11e-30kg), dt (unité de temps d'intégration), xx=echelle des longueurs 1cm=xx fm(= xx e-15m), nb entier coeff de calcul graphique des accélérations (environ -27), point N, point M0, vecteur Vo |
| Objets finaux : points M1 à M10, vecteurs v10 et F10 . |
Appliquée 5 fois, on obtient,

pour créer la macro
| Définition de la macro construction EulerQ50p5v.mac : ( ordre 1, Q Coulomb, 50 pour les 50 points, 5 vecteurs vitesses) |
| Objets initiaux : qN, qM (nb de charge en unité 1.6e-19C), nme = masse de la particule mobile en unité de masse de l'électron 9.11e-30kg), dt (unité de temps d'intégration), xx=echelle des longueurs 1cm=xx fm(= xx e-15m), nb entier coeff de calcul graphique des accélérations (environ -27), point N, point M0, vecteur Vo |
| Objets finaux : points M1 à M50, 5 vecteurs v10 à v50 . |
-------------------------------------------
Méthode d'Euler ordre 2
On reprend les mêmes calculs,
Les relations importantes :
Force électrostatique subie par la charge q de masse m située au point M
: F = 9.0e9 q q' / r2 r/r, la force est attractive dirigée vers le noyau N portant
la charge q', si q et q' sont de signe contraire, ou dirigée dans la direction NM si q et q' sont de même
signe.
Dans l'expérience initiale de Rutherford, q est un proton, et q' un noyau d'or (force répulsive).
F = m a = m dv/dt et F = 9.0e9 q q' / r2 r/r soit a = 9.0e9
q q' /( m r2 ) r/r
Puisqu'on connait le vecteur accélération, on peut écrire : r1 = ro + vo
dt + ao dt2 /2 au deuxième ordre.
v1 = vo + ao dt
Unités : Les grandeurs utilisées ici ne sont pas adaptées aux dessins, aussi les variables
seront le nombre de charges élémentaires (1,6e-19C), les distances en femtomètre (10-15m)
et les masses exprimées par rapport à la masse d'un électron (me=9,11e-31kg).
L'accélération s'écrit alors a = 2.52e32 qN qM / (nme r2) où
qN = q / 1,6e-19C pour le noyau,
qM = q / 1,6e-19C et nme = masse / 9,11e-31kg pour la charge mobile
r = distance (NM) en femtomètre.
Valeurs typiques : qN = 79, qM = 1, nM = 1835, r = 100 fm
Construction (identique au premier ordre) :
- Tracer 4 segments, sur des droites horizontales, qui représentent qN , qM, nme, et l'intervalle de
temps dt.
On utilisera la longueur de ces segments comme paramètres dans les calculs suivants, (multipliés
éventuellement par un coefficient pour les échelles).
- Placer les points N (Noyau) et Mo (position initiale dde la charge q)

- Tracer le vecteur vo, vitesse initiale du point Mo.
Ce vecteur peut avantageusement être créé autour d'un point fixe afin de rendre
sa manipulation plus facile. Il faut alors le reporter en Mo.
- Mesurer la distance ro=distance (T Mo) et la longueur vo du vecteur vo.

- Calculer ao= 2.52e32 qN qM / (nme r2) et comme on obtient un nombre très grand (1025 à 1028 environ), on multiplie ce résultat par 10-27 par exemple. De même la vitesse sera multipliée par un coefficient, (10 000 000 pour 1cm = 10 000 km/s)

- Tracer la demi-droite (Mo N), pour définir la direction du vecteur Fo.
- Calculer la grandeur vo dt, et la reporter sur la demi-droite (Mo vo), pour définir le point M'
- Calculer la grandeur ao dt2 /2, et la reporter sur la demi-droite (Mo N') où N' est le symétrique de N par rapport à Mo, pour définir le point M''
- Calculer la grandeur ao dt, et la reporter sur la demi-droite (Mo N') , pour définir le vecteur (ao
dt)
v1 = vo + ao dt
v1 est obtenu par addition vectorielle de vo et ao dt au point M1, qui n'est plus sur la demi-droite
(Mo vo) , comme dans l'approximation d'ordre 1.
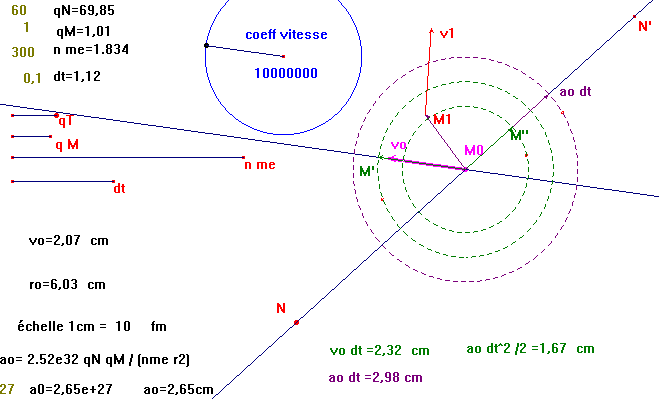
On peut alors définir les différentes macros.
| Définition de la macro construction Euler2Q1 : ( 2 pour ordre 2, Q charge (Coulomb), 1 pour 1 vecteur) |
| Objets initiaux : qN, qM (nb de charge en unité 1.6e-19C), nme = masse de la particule mobile en unité de masse de l'électron 9.11e-30kg), dt (unité de temps d'intégration), xx=echelle des longueurs 1cm=xx fm(= xx e-15m), nb entier coeff de calcul graphique des accélérations (environ -27), point N, point M0, vecteur Vo |
| Objets finaux : point M1, vecteur v1 |
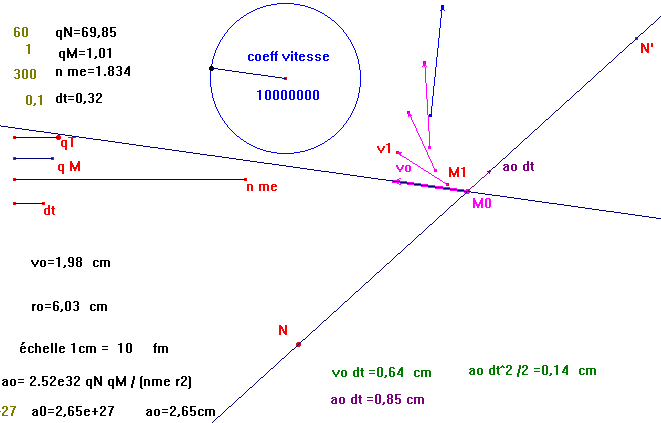
A partir de cette macro, on peut en définir une seconde qui trace 4 points successifs et la conique définie
par les 5 points Mo à M4 (avec l'outil Conique de Cabri).
| Définition de la macro construction Euler2Q1_4pv_cnk.mac : ( 2 pour ordre 2, 1Q charge (Coulomb), 4 points et 4 vecteurs, conique des 5 points) |
| Objets initiaux : qN, qM (nb de charge en unité 1.6e-19C), nme = masse de la particule mobile en unité de masse de l'électron 9.11e-30kg), dt (unité de temps d'intégration), xx=echelle des longueurs 1cm=xx fm(= xx e-15m), nb entier coeff de calcul graphique des accélérations (environ -27), point N, point M0, vecteur Vo |
| Objets finaux : M1 à M4 et vecteur v1 à v4 et la conique des 5 pts M0 à M4 |
Après un peu de nettoyage,
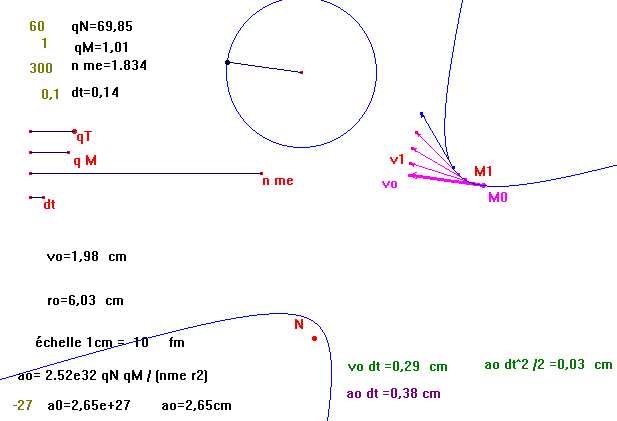
Pour placer plusieurs (10) points on peut définir la macro
| Définition de la macro construction Euler2Q10v.mac : ( ordre 2, Q Coulomb, 10 pour les 10 points et vecteurs vitesses) |
| Objets initiaux : qN, qM (nb de charge en unité 1.6e-19C), nme = masse de la particule mobile en unité de masse de l'électron 9.11e-30kg), dt (unité de temps d'intégration), xx=echelle des longueurs 1cm=xx fm(= xx e-15m), nb entier coeff de calcul graphique des accélérations (environ -27), point N, point M0, vecteur Vo |
| Objets finaux : points M1 à M10, vecteurs v1 à v10 . |
| Définition de la macro construction Euler2Q10p1v.mac : ( ordre 2, Q Coulomb, 10 pour les 10 points et 1 vecteur vitesse) |
| Objets initiaux : qN, qM (nb de charge en unité 1.6e-19C), nme = masse de la particule mobile en unité de masse de l'électron 9.11e-30kg), dt (unité de temps d'intégration), xx=echelle des longueurs 1cm=xx fm(= xx e-15m), nb entier coeff de calcul graphique des accélérations (environ -27), point N, point M0, vecteur Vo |
| Objets finaux : points M1 à M10, vecteurs v10 . |
Appliquée 5 fois, on obtient,
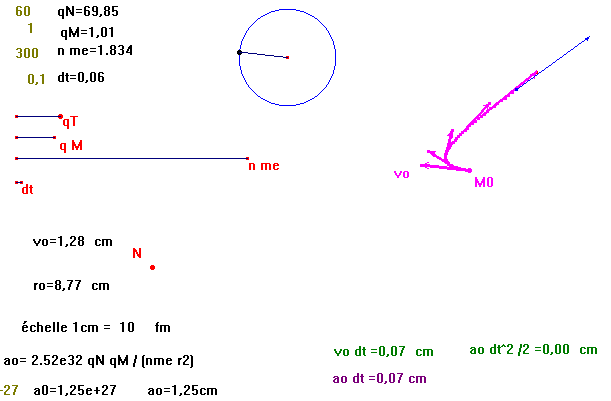
pour créer la macro
| Définition de la macro construction Euler2Q50p5v.mac : ( ordre 2, Q Coulomb, 50 pour les 50 points, 5 vecteurs vitesses) |
| Objets initiaux : qN, qM (nb de charge en unité 1.6e-19C), nme = masse de la particule mobile en unité de masse de l'électron 9.11e-30kg), dt (unité de temps d'intégration), xx=echelle des longueurs 1cm=xx fm(= xx e-15m), nb entier coeff de calcul graphique des accélérations (environ -27), point N, point M0, vecteur Vo |
| Objets finaux : points M1 à M50, 5 vecteurs v10 à v50 . |
-------------------------------------------
Méthode Cabri Géomètre exacte.
Les relations importantes :
Force électrostatique subie par la charge q de masse m située au point M
: F = 9.0e9 q q' / r2 r/r, la force est attractive dirigée vers le noyau N portant
la charge q', si q et q' sont de signe contraire, ou dirigée dans la direction NM si q et q' sont de même
signe.
Dans l'expérience initiale de Rutherford, q est un proton, et q' un noyau d'or (force répulsive).
F = m a = m dv/dt et F = 9.0e9 q q' / r2 r/r soit a = 9.0e9
q q' /( m r2 ) r/r
Unités : Les grandeurs utilisées ici ne sont pas adaptées aux dessins, aussi les variables
seront le nombre de charges élémentaires (1,6e-19C), les distances en femtomètre (10-15m)
et les masses exprimées par rapport à la masse d'un électron (me=9,11e-31kg).
L'accélération s'écrit alors a = 2.52e32 qN qM / (nme r2) où
qN = q / 1,6e-19C pour le noyau,
qM = q / 1,6e-19C et nme = masse / 9,11e-31kg pour la charge mobile
r = distance (NM) en femtomètre.
Valeurs typiques : qN = 79, qM = 1, nM = 1835, r = 100 fm
L'accélération normale à la trajectoire est aN= vo2 / Rayon de courbure.
Le centre de courbure C définit le cercle osculateur de la conique au point Mo.
Cabri Géomètre peut construire la conique définie par un foyer et le cercle osculateur en un point.
Construction :
- Tracer 3 segments, sur des droites horizontales, qui représentent qN , qM, nme.
On utilisera la longueur de ces segments comme paramètres dans les calculs suivants, (multipliés
éventuellement par un coefficient pour les échelles).
- Placer les points N (Noyau) et Mo (position initiale dde la charge q)
- Tracer le vecteur vo, vitesse initiale du point Mo.
Ce vecteur peut avantageusement être créé autour d'un point fixe afin de rendre
sa manipulation plus facile. Il faut alors le reporter en Mo.
- Créer deux nombres pour les échelles de longueur (50 pour 1cm=50fm)
et de vitesse (10 000 000)
- Mesurer la distance ro=distance (N Mo) et la longueur vo du vecteur vo.
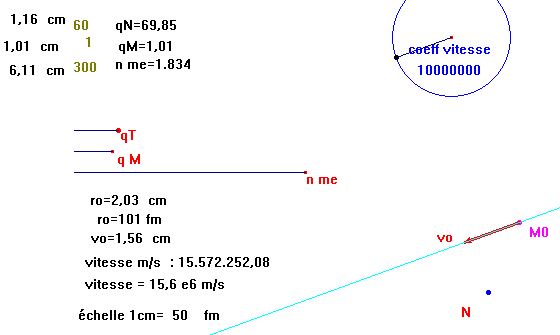
- Calculer ao= 2.52e32 qN qM / (nme ro2) , on obtient un nombre de l'ordre de 1026. Pour reporter le vecteur ao, il faut le mettre à la dimension du dessin, ao sera multiplié par la quantité 10(-floor( log(ao))), la mesure résultante sera comprise ainsi entre 1 et 10 cm.
- Reporter ao sur la demi-droite (Mo N), pour définir le vecteur ao , (Voir remarque plus loin)
- Tracer la perpendiculaire à (Mo vo) = normale à la trajectoire au point Mo ,
- Projeter l'extrémité de ao sur cette normale pour obtenir aN et sa longueur aN
.
- Calculer le rayon de courbure par R=vo2/aN et placer le point C , centre du cercle osculateur sur
la demi-droite (Mo aN) .
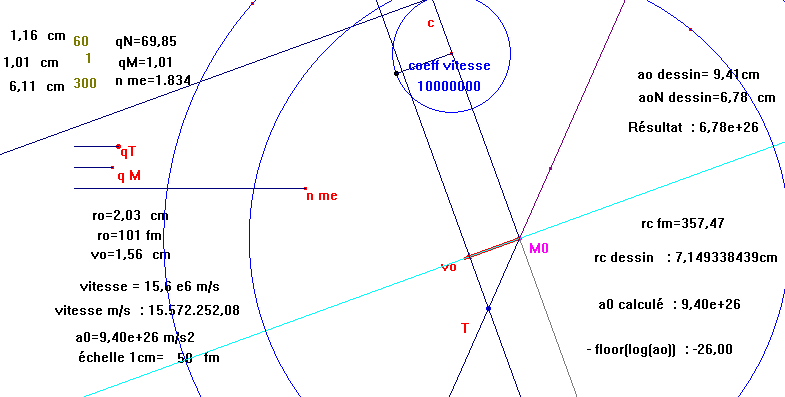 (FigQ_02.fig)
(FigQ_02.fig)
- Tracer le cercle passant par Mo et C dont le centre est le milieu de MoC. Ce cercle coupe la demi-droite MoT au point P
- Tracer la perpendiculaire à MoC passant par P , Q est la projection orthogonale de P sur MoC
- Tracer la droite passant par T et Q,
- P' est le le symétrique de P par rapport à la droite MoC,
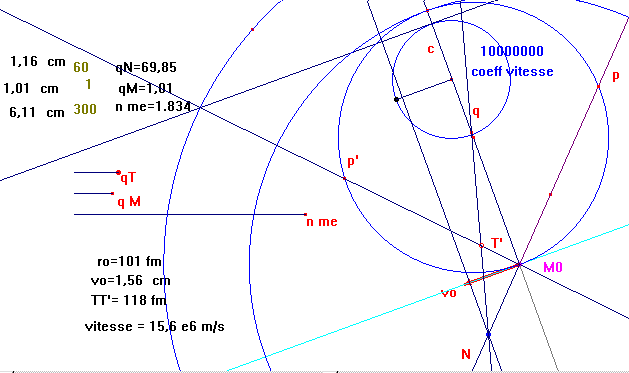 (figQ_03.fig)
(figQ_03.fig)
- Tracer la droite passant par Mo et P' ,
- Les droites TQ et MoP' se coupe au deuxième foyer T'.
- Utiliser la macro "Conique par 2Foyers et une tangente"
(http://www-cabri.imag.fr/abracadabri/Coniques/BiFocale/PropBiFocale/FigBFIntro/Cnk2F1Tg.mac par exemple chez Y. Martin) pour obtenir la conique résultante. Attention , la droite qui sert dans la définition de la macro est définie après la construction du vecteur vo et non avant vo (ce qui peut arriver si on utilise comme ici une construction auxiliaire pour la définition de vo).
La trajectoire de la charge qM est la conique obtenue. Il s'agit d'une solution exacte (mais qui exclu la parabole).
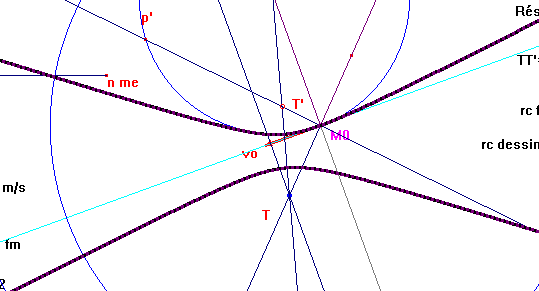 (figQ_04.fig)
(figQ_04.fig)
Pour conserver seulement une partie de la conique on peut par exemple définir un segment par les points
M0 et ST', avec le point SM0T' symétrique de M0 par rapport à NT', puis ST' symétrique de
T' par rapport à SM0T' . La demi-droite NX, (le point X est sur le segment M0 ST'). coupe l'hyperbole .
Le lieu de ce point lorsque X se déplace sur le segment visualise une portion de la trajectoire de la charge
qM.
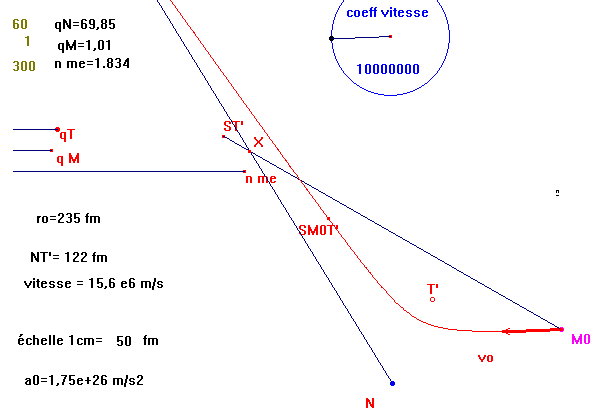 (figQ_06.fig)
(figQ_06.fig)
Après nettoyage, en conservant seulement une partie de la branche intéressante de la conique,
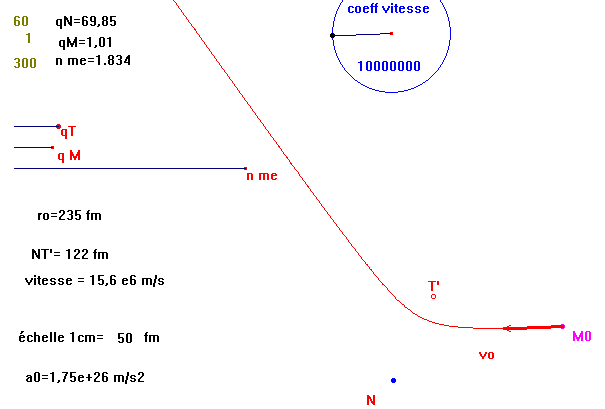 (figQ_05.fig)
(figQ_05.fig)
| Définition de la macro construction Coulomb_ech_fm_1a : |
| Objets initiaux : Montrer qN, qM (nb de charge en unité 1.6e-19C), nme = masse de la particule mobile en unité de masse de l'électron 9.11e-30kg), xx=echelle des longueurs 1cm=xx fm(= xx e-15m), yy=echelle vitesse 1cm= xx m/s (environ 10e6 ou 10e7), point N, point M0, vecteur Vo, |
| Objets finaux : 2 branches de la conique, lieu sur la bonne branche et deuxième foyer |
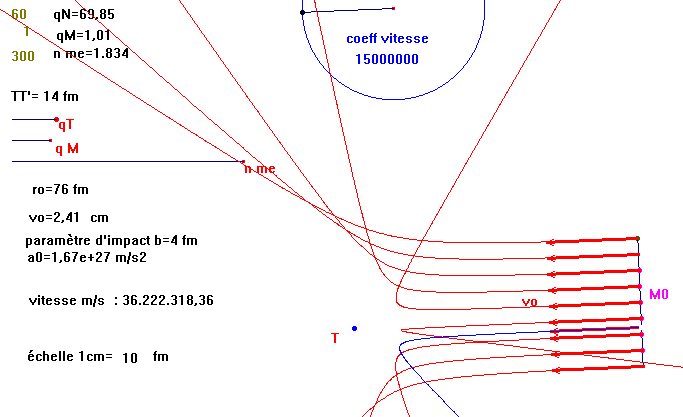
FigQd28_ok.fig
avec la macro
| Définition de la macro construction Coulomb_ech_fm_8l : |
| Objets initiaux : Montrer qN, qM (nb de charge en unité 1.6e-19C), nme = masse de la particule mobile en unité de masse de l'électron 9.11e-30kg), xx=echelle des longueurs 1cm=xx fm(= xx e-15m), yy=echelle vitesse 1cm= xx m/s (environ 10e6 ou 10e7), nb entier coeff de calcul graphique des accélérations (environ -25), point T, point M0, vecteur Vo, point extreme sur un segment perpendiculaire au vecteur Vo, un point mobile sur le segment, |
| Objets finaux : lieux sur la bonne branche huit fois |

On peut ainsi obtenir :
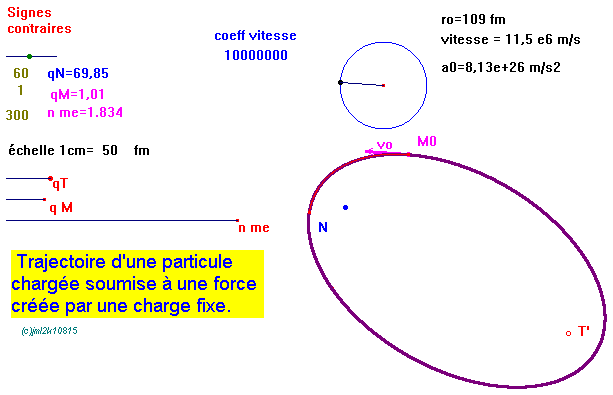
ou

FigQ_auto_pm.fig
On peut définir une nouvelle macro
| Définition de la macro construction Coulomb_ech_fm_1pm : |
| Objets initiaux : Montrer qN, qM (nb de charge en unité 1.6e-19C), nme = masse de la particule mobile en unité de masse de l'électron 9.11e-30kg), xx=echelle des longueurs 1cm=xx fm(= xx e-15m), yy=echelle vitesse 1cm= xx m/s (environ 10e6 ou 10e7), nombre positif si les charges sont de meme signe (négatif sinon), point N, point M0, vecteur Vo, |
| Objets finaux : 2 branches de la conique et deuxième foyer |
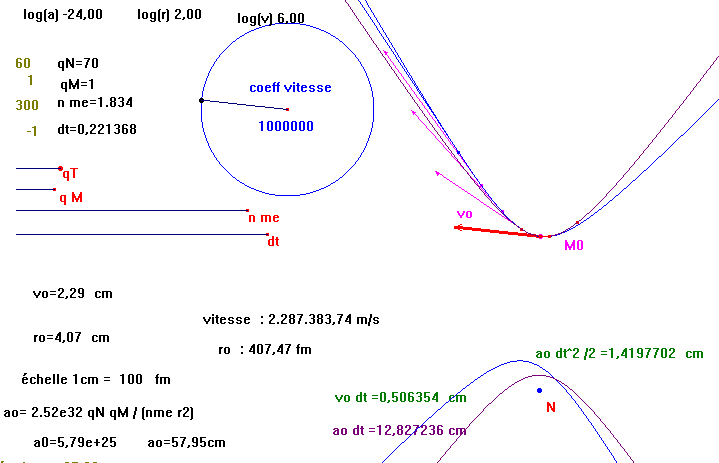
mais avec un dt suffisament petit, les deux coniques sont parfaitement superposées
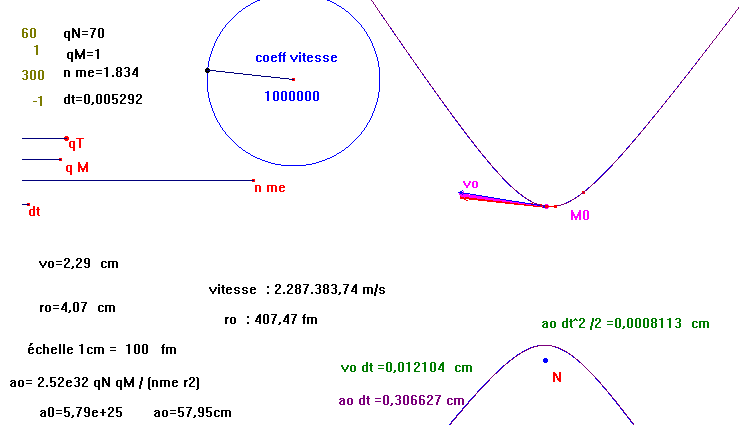
comparaison echelleFigQ_euler2_auto_fin.fig
Conclusion :
Si l'intervalle d'intégration ou de discrétisation temporelle est suffisament faible, la méthode
d'Euler permet d'obtenir un très bon résultat.