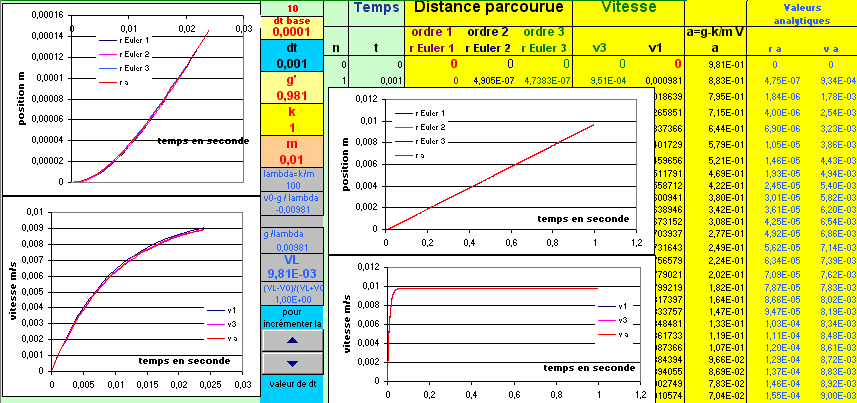
dt=9.5ms
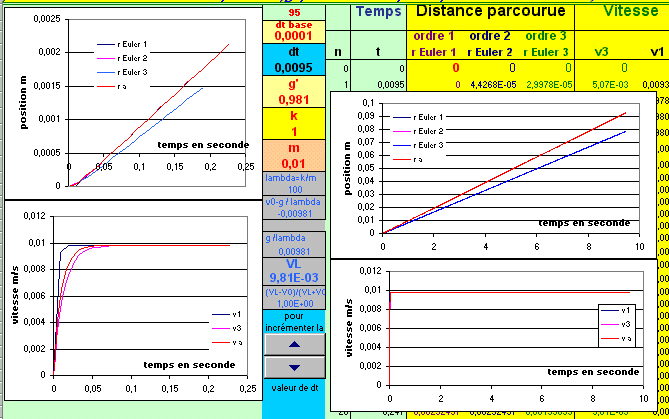
Cas où la force est F3=-k v .
Méthode d'Euler
La masse est soumise aux deux forces F1 et F3.
L'accélération ao est ao = g - k v/m et
dao/dt = - 2 k/m dv/dt = -2 k /m ( g - k v/m)
La vitesse limite VL est VL = mg/k = g/ l avec l = k/m
On calculera donc selon le cas :
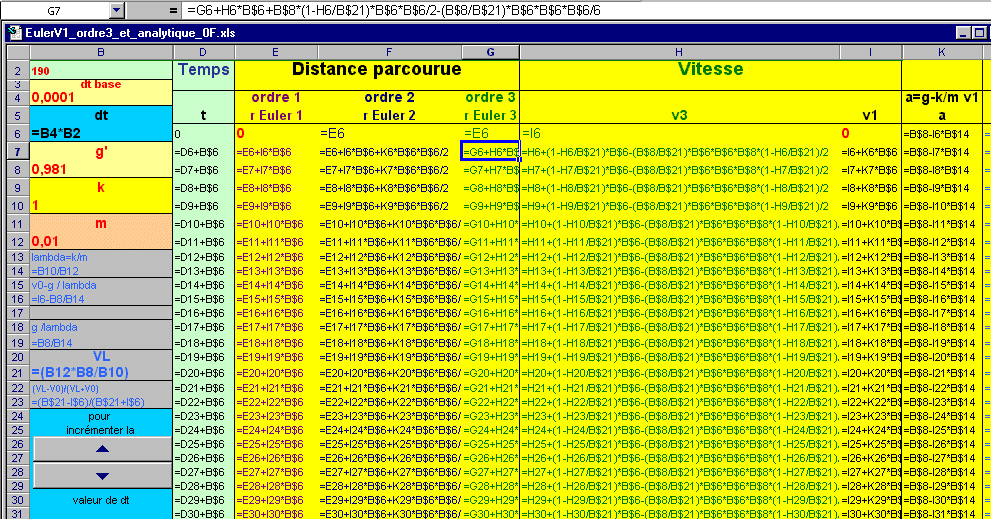
r1 = ro + vo dt et v1 = vo + g ( 1 - v0/VL) dt
ou
r2 = ro + vo dt + g ( 1 - v0/VL) dt2 /2 et v1 = vo + g ( 1 - v0/VL)
dt
ou
r3 = ro + vo dt + g ( 1 - v0/VL) dt2 /2 - g dt3 /(6
VL)
et v3 = vo + g ( 1 - v0/VL) dt - g2 ( 1 - v0/VL)/ (2 VL) dt2
Méthode analytique.
L'équation différentielle en v :
dv/dt = g (1 -v/VL)
s'intègre en :
v = VL - (VL - v0) exp(-l t) avec VL = mg/k et l = k/m
et la position est donnée par l'expression :
r = (v0-VL)(1-exp(- l t)) / l +VL t + r0
Comparaison des deux méthodes avec un tableur :
Comme dans le cas précédent, les différentes formules sont entrées dans les cellules
du tableur.
Données :
|
Cellule |
fonction |
valeur typique au départ |
| B2 | delta t , incrément obtenu avec l'action des boutons "Compteur" | 10 |
| B4 | unité de temps de base | 0.0001 |
| B8 | accélération de la pesanteur locale, s'il faut tenir compte dele poussée d'Archimède, g'<g | 9.81 |
| B10 | coefficient de frottement USI | 1 |
| B12 | masse en kg | 0.01 |
| E6 | position à t=0 | 0 |
| I6 | vitesse à t=0, si <0 alors départ vers le haut | 0 |

dt=1ms

dt=9.5ms

dt=19ms
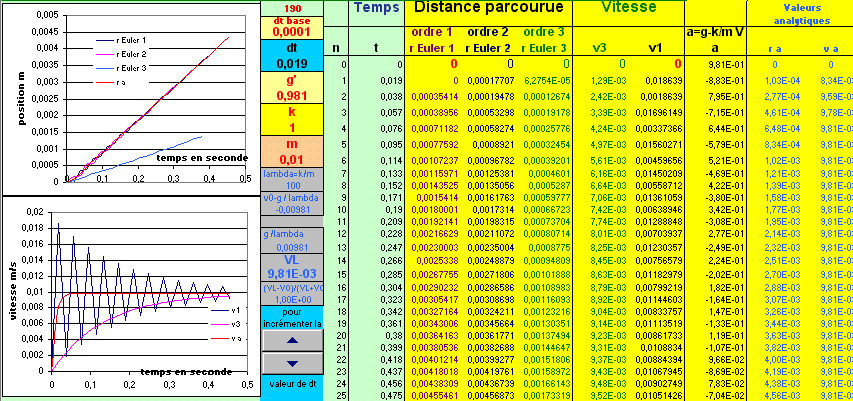
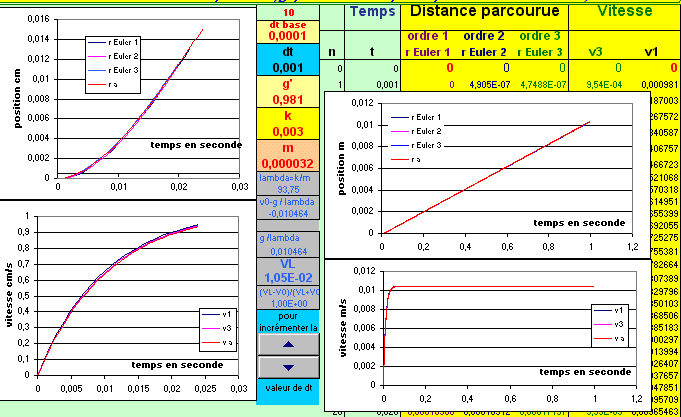
Conclusion :
Ici la vitesse tend vers une valeur limite avec un régime transitoire très court, après 20ms
la vitesse est déjà à 80% de la valeur limite. Il faut que la discrétisation temporelle
soit suffisament courte pour que la méthode d'Euler soit acceptable.
C'est le cas lorsque dt=1ms , avec dt=9.5ms, les erreurs sont importantes et pour dt=19.5ms (voisin du temps caractéristique
du phénomène étudié), la méthode ne converge plus.
Retour sur une expérience de seconde.
Un exemple rencontré en classe de seconde, avec la chute d'une gouttelette d'eau dans de l'huile ; pour
un rayon de 2mm environ, la vitesse observée est (peut être suivant les conditions expérimentales)
de 1cm/s, on obtient les résultats suivants (avec les courbes des positions en cm et vitesse en cm/s pour
les faibles distances).
fichier (100 points) tableur compressé 116ko
(pour avoir 1000 points recopier la dernière ligne jusqu'à la ligne 1006)
Ces résultats peuvent être retrouvés avec la simulation de Cabri Géomètre :
Ce que l'on peut voir avec la séquence filmée d'une goutte d'eau (208ko)colorée au KMnO4 qui tombe dans de l'huile (de soja).
Avec les paramétres, VL=1.4cm/s et une viscosité =7.10-3 kg m-1 s-1
environ, pour une masse volumique de 9.102kg m-3 , le rayon de la goutte r=2mm après
exploitation avec Synchronie2000.
Caméra : webcam USB ToUCam Philips 740, 5 images par seconde, compression reprise avec VirtualDub, Indeo 504 à 50%