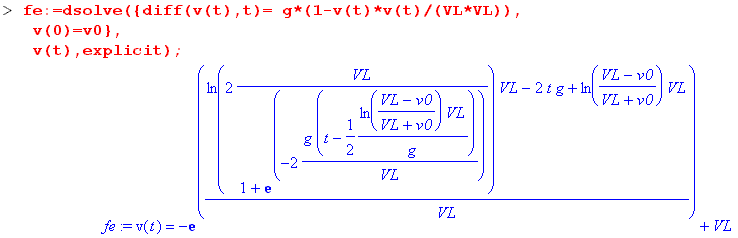
Cas où la force est F2=-k v² v/v .

Méthode d'Euler

La masse est soumise aux deux forces F1 et F2.

L'accélération ao est ao = g - k v²/m et
dao/dt = - 2 k v dv/dt = -2 k v ( g - k v²/m) /m

On calculera donc selon le cas :

r1 = ro + vo dt et v1 = vo + ao dt
ou
r2 = ro + vo dt + ( g - k v²/m) dt² /2 et v1 = vo +( g - k v²/m) dt
ou
r3 = ro + vo dt + ( g - k v²/m) dt² /2 - ( 2 k v ( g - k v²/m) /m ) dt³ /6
et v3 = vo + ao dt -2 k/m ( g - k v²/m) v dt²

Méthode analytique.

Avec l'aide de Maple,

Les équations différentielles pour la vitesse et la position sont obtenues à partir de l'expression :

après simplification , la vitesse peut se mettre sous la forme :

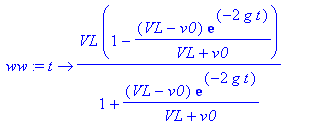
Une intégration permet d'obtenir la position sous la forme :

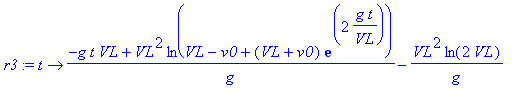
Le terme VL² ln(2VL)/g correspond à la constante d'intégration r3(0) qu'il faut enlever à la fonction obtenue par l'intégration.

Comparaison des deux méthodes avec un tableur :

Avec Excel par exemple, dans le cas le plus général, vitesse initiale et position initiale non nulles (v(t=0) est dirigée vers le haut et r(t=0)=0)
Les données modifiables sont en rouge.

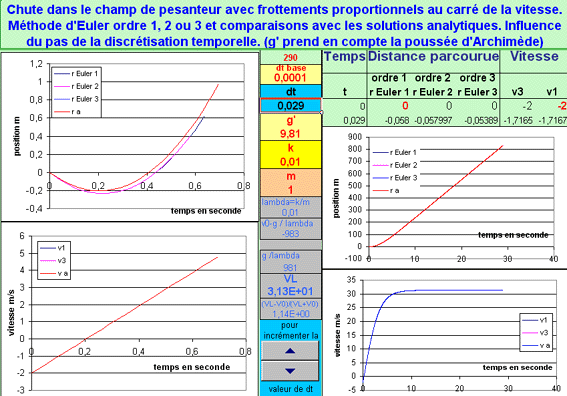
ou avec les erreurs relatives

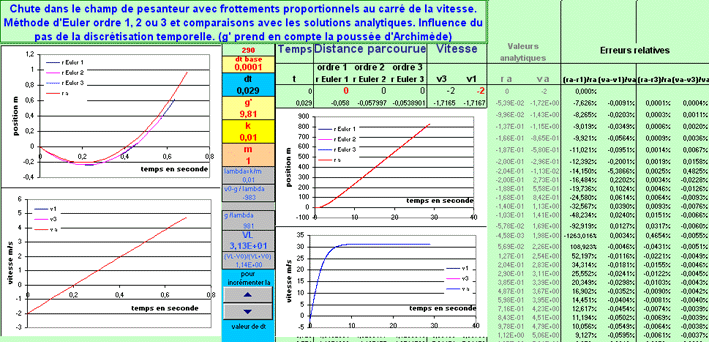
Données :

Cellule	fonction	valeur typique au départ
B2	delta t , incrément obtenu avec l'action des boutons "Compteur"	10
B4	unité de temps de base	0.0001
B8	accélération de la pesanteur locale, s'il faut tenir compte dele poussée d'Archimède, g'<g	9.81
B10	coefficient de frottement USI	0.01
B12	masse en kg	1
E6	position à t=0	0
I6	vitesse à t=0, si <0 alors départ vers le haut	0

Saisir les formules pour les calculs.
Les cellules B14, B16, B19, B21, B23 contiennent des paramètres utilisés dans les formules de calcul principales.
Taper les formules suivantes dans les cellules D à Q de la ligne 7

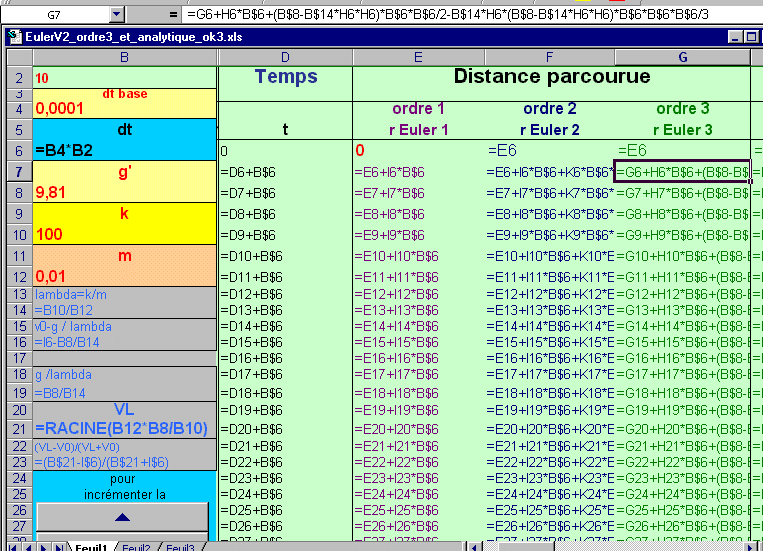
puis

et M7==B$21*(1-B$23*EXP(-2*B$8*D7/B$21))/(1+B$23*EXP(-2*B$8*D7/B$21))

et incrémenter jusqu'à la ligne 1006 par exemple.

Le compteur permet de modifier la valeur de dt facilement. Il utilise une petite macro créée automatiquement par Excel à la création de ce compteur. Il peut être supprimé, mais il faudra alors saisir les valeurs du compteur dans la cellule B2, ou spprimer la formule de B6 et saisir les valeurs de dt dans la cellule B6.

Exploitation :
Cas du parachutiste de masse 80kg, coefficient de frottement 80kg/m avec :
dt=0.001s


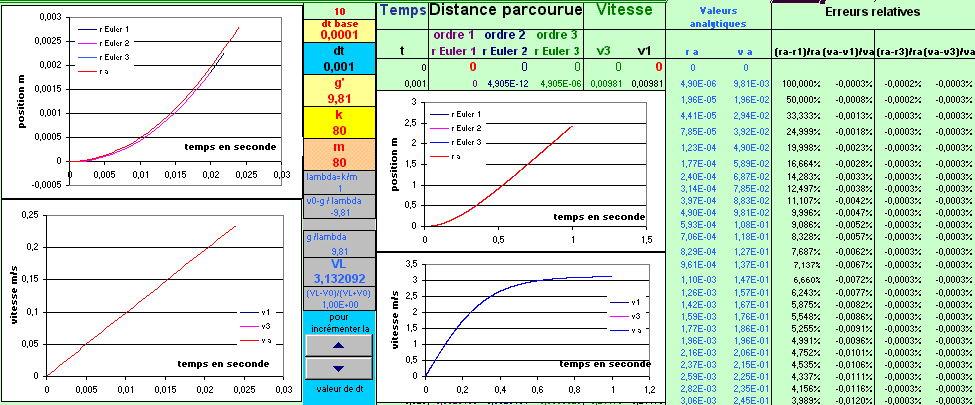
et dt=0.1s

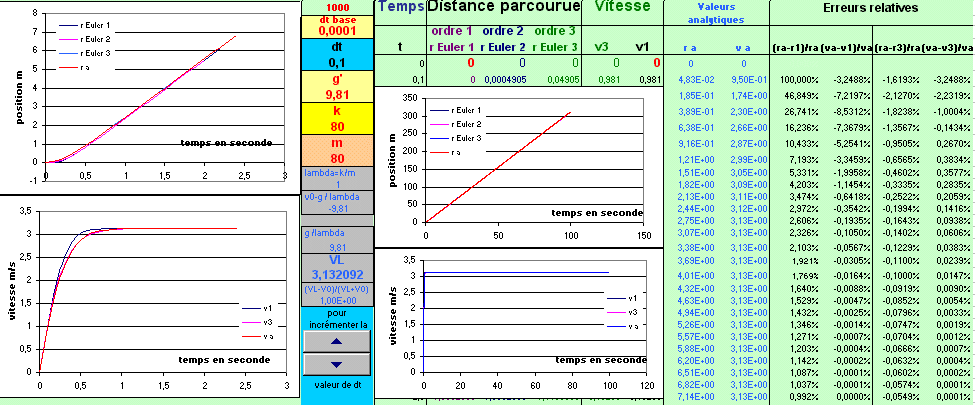
fichier (1000 points) tableur compressé 151ko

Conclusion :
Les erreurs relatives ne sont jamais négligeables pour la position à l'ordre 1 .
Les erreurs relatives sont négligeables pour la position et la vitesse pour dt=0.001 à l'ordre 3 et pour la vitesse à l'ordre 1.
Les erreurs relatives sont inférieures à 4% pour la position et la vitesse pour dt=0.1 à l'ordre 3 et pour la vitesse sont inférieures à 9% à l'ordre 1(maximum vers t=0.3s).

Retour Présentation
Cas où la force est F3=-k v .